El autor analiza las propiedades matemáticas del sistema electoral y muestra cómo premia a las listas fuertes: aquellas que reúnen conglomerados políticos y candidatos y candidatas con alta votación. La fragmentación de quienes quieren el cambio podría significar que en las elecciones de constituyentes triunfe fácilmente la derecha o las mismas caras de siempre.
Las afirmaciones planteadas en esta columna se fundamentan, entre otras fuentes, en una serie de proyectos interdisciplinarios en los que he participado: (1) Proyecto ANILLO SOC-17 (2008-2011), La educación ante el riesgo de fragmentación social: ciudadanía, equidad e identidad nacional. Co-investigador en el análisis de los censos del siglo XIX, lo que permitió investigar los censos electorales y el sentido electoral de los censos en general; (2) Proyecto FONDEDOC 200/2007 (2007-2008), Matemática Electoral: Del Problema Político a la Solución Matemática. Investigador principal; (3) Proyecto Interdisciplinario (2008-2009), Una historia social de las elecciones a través de los números: la representación ciudadana entre 1810 y 1891. Investigador principal. (4) Proyecto FONDECYT 1181261 (2018-2021), Ignoring Ignorability: Towards a Realistic Educational Research. Investigador Principal.
El 25 de octubre, los ciudadanos que asistieron a votar optaron por una Convención Constitucional (CC) como el órgano redactor de la Nueva Constitución. De acuerdo a la ley, la CC estará integrada por 155 ciudadanos elegidos por votación popular. Para algunos actores, dichos ciudadanos deben provenir de organizaciones y movimientos sociales no adscritos a los actuales partidos políticos, pues los resultados del plebiscito refrendan el rechazo que la ciudadanía tiene por los partidos. Para otros, esos ciudadanos deben pertenecer a los partidos, a condición de ser nuevos rostros, pues una democracia requiere un amplio abanico de representantes. Cualquiera sea la interpretación, el objetivo de corto plazo es la elección de los convencionales. De acuerdo al artículo 141 de la Ley 21.200, se escogerán tantos convencionales como diputados se eligen en los distritos electorales. Para ello se utilizará el mismo sistema que rige la elección de diputados y senadores[1]. El objetivo de esta columna es mostrar y analizar las propiedades matemáticas de ese sistema; propiedades que hacen que el sistema tenga una característica esencial: promueve las listas fuertes, es decir aquellas cuyos candidatos/as concitan una gran cantidad de votos.
En nuestro sistema electoral, una lista es un conjunto de candidatas y candidatos que representan un determinado interés político. Por las características del sistema, el acento está puesto en la lista: la asignación de escaños es proporcional a la cantidad de votos que obtiene la lista en una determinada elección. De entre los métodos de asignación parlamentaria (Huntington, 1921; 1928; Pukelsheim, 2014), nuestro sistema utiliza el coeficiente de D’Hondt, un método introducido por el abogado belga Víctor D’Hondt (1882). Este nos ha acompañado en Chile al menos desde 1912, cuando la Juventud Liberal de Chile empujó su adopción (Maza, 1913). Fue conocido tradicionalmente como Método de Cifra Repartidora y rigió la asignación de escaños después de 1925. De hecho, el Sistema Binominal corresponde al método de D’Hondt pero aplicado para asignar dos escaños.
Para las listas que tienen proporciones de votos 'altas' (mayores, por ejemplo, al 50%), sobrepasar los umbrales de representación se hace 'más fácil' a medida que compiten muchas listas, no así para las listas ‘pequeñas'
Ante la preocupación que los actores políticos tienen de cara a la elección de convencionales, resulta relevante enfatizar que cada método proporcional satisface ciertas propiedades matemáticas que tienen una directa interpretación política. En lo que se refiere al método de D’Hondt, hay dos propiedades que permiten afirmar que este método asegura cierta estabilidad política, pues impide la atomización de la representación en el Congreso Nacional:
El método de D’Hondt alienta las coaliciones políticas: si dos listas que compiten por separado hubiesen competido como lista única, obtienen al menos una cantidad de escaños igual a la suma de escaños que ambas listas obtuvieron por separado. Un ejemplo de esto ocurrió en el distrito 11 en la elección de diputados de 2017[2]: las listas N (esencialmente PPD y PS) y O (DC) no obtuvieron escaños. Pero, si hubiesen ido juntas, y asumiendo que los electores se hubiesen comportado como efectivamente lo hicieron en cuanto a sus votos, habrían obtenido 1 escaño, dejando a Chile Vamos con 4 escaños, y RD más el PH con 1.
El método de D’Hondt es un sistema proporcional que no respeta la cuota. Para ilustrar este punto, volvamos a la elección de 2017 y al distrito 11. En esa elección, Chile Vamos obtuvo el 63% de los votos válidamente emitidos en el distrito 11. Allí se eligen 6 representantes, por lo que la cuota exacta de la lista Chile Vamos es igual a 3.78 escaños. Los sistemas proporcionales se caracterizan por el modo en que redondean estas cuotas (Balinski & Youg, 1975; Birkhoff, 1076). Se dice que un método proporcional respeta la cuota si asigna un número de sillas al menos igual a la parte entera de la cuota exacta, y a lo más igual a dicha parte entera más uno. En el ejemplo, esto equivaldría a asignar 3 ó 4 escaños. Sin embargo, y este es el punto que debemos tener en cuenta, el método de D’Hondt le asignó 5 escaños a Chile Vamos, pues este método es un sistema proporcional que no respeta la cuota[3].
Estas propiedades resultan relevantes a la hora de conformar listas para elegir convencionales para la CC. De hecho, lo que sugiere el método de D’Hondt es que se requieren listas “fuertes”, es decir, listas que conciten una gran cantidad de votos, lo que a su vez significa asociarse en torno a ideales e intereses políticos lo más transversales posibles.
Tal vez esta constatación no parezca un impedimento para que la mayoría que se pronunció el 25 de octubre quede representada por la mayoría de convencionales. De hecho, se repite una y otra vez que la mayoría de las y los ciudadanos quieren que la Nueva Constitución sea redactada por una CC. Pero es necesario atenerse a las verdades de hecho[4] que el plebiscito manifestó: solo el 50.09% de los electores residentes en Chile asistieron a votar y, de ellos, el 19.88% optó por una Convención Mixta Constitucional (CMC) como órgano redactor de la Nueva Constitución, mientras que el 74.73% optó por una CC[5]. Tomando en cuenta esos resultados, solo podemos afirmar que al menos un 37.43% de los chilenos opta por una CC (y por tanto un 59.87% por la CMC) y que a lo más el 87.43% opta por la CC (y por tanto un 9.96% por la CMC). Esto, suponiendo que los que no asistieron a votar habrían optado por CC o por CMC. Un análisis como éste puede hacerse para cada distrito (para detalles, ver San Martín 2020b)[6].
Como se puede constatar, existe un amplio margen de posibilidades de intenciones de votos, asumiendo que el comportamiento de los electores el 25 de octubre y las intenciones de voto del 11 de abril próximo serán políticamente coherentes entre sí. Por tanto, nada es seguro y cualquier simulación de posibles escenarios debe transparentar los supuestos que, al final del día, son creencias, ya sea que provengan del político, del científico o del ciudadano.
ESCENARIOS POSIBLES EN LA FUTURA ELECCIÓN DE CONVENCIONALES
Hasta ahora he abordado las incertezas que caracterizan el proceso. A continuación, mostraré que, si los escaños son asignados usando el método de D’Hondt, es posible cuantificar la proporción mínima de votos que requiere una lista para elegir convencionales, lo cual depende esencialmente del número de representantes que se elige en un distrito. Además, mostramos cómo este resultado se complementa si se tiene en cuenta el número de listas que compiten. Esta información resulta útil para visualizar distintos escenarios electorales. Para esta demostración usaré funciones que, en el método de D’Hondt, muestran la relación entre proporciones de votos necesarios para obtener escaños con el total de escaños a repartir y las listas que compiten.
La idea es la siguiente:
Si H denota el total de escaños a repartir en un distrito y n el total de listas que compiten, los siguientes umbrales
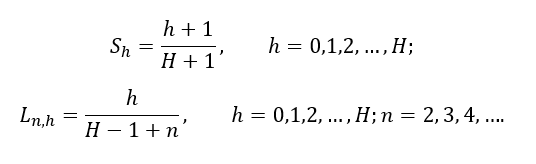
satisfacen, para el método de D’Hondt, las siguientes propiedades:
Si una lista obtiene una proporción de votos menor que Ln,h, entonces es seguro que recibirá menos de h sillas. En particular, si la lista obtiene una proporción de votos menor que Ln,1, es seguro que no obtendrá representación alguna. Por ello, Ln,1 se llama umbral de representación (Lijphart & Gibberd, 1977).
Si una lista obtiene una proporción de votos mayor que Sh,, entonces es seguro que recibirá menos de h sillas. En particular, si la lista obtiene una proporción de votos mayor que S0, entonces es seguro que recibirá al menos 1 escaño. Por ello, S0 se llama umbral de exclusión (Lijphart & Gibberd, 1977).
Si una lista obtiene una proporción de votos en el intervalo [Ln,h,Sh,], entonces es solo probable que la lista obtenga h sillas. [7]
La tabla a continuación nos permite analizar distintos escenarios para el caso que se asignan H=7 (como es el caso de los distritos 5, 9, 12, 17 y 23)[8]: las celdas de la tabla contienen los respectivos umbrales Ln,h, para el caso que compitan 2, 3, 4, 5, 6 y 7 listas, además de los umbrales Sh.
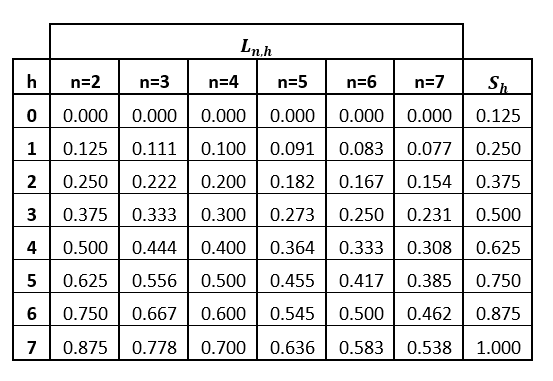Así, por ejemplo, si una lista obtiene menos del S0 = 1,25% de los votos[9], entonces es seguro que no obtendrá escaño alguno. Si obtiene, por ejemplo, una proporción de votos mayor que S2 = 37.5% de los votos, es seguro que obtendrá más de dos representantes. Los umbrales Sh expresan cuán difícil es obtener más de h sillas; es más, esta dificultad no depende del número de listas que compiten.
Por otro lado, los umbrales de representación Ln,1 disminuyen a medida que compiten más listas: si compiten 3 listas, las que obtienen menos del 11.1% de los votos no tendrán representación; si son 4 listas, las que obtienen menos del 10% de los votos no tendrán representación; si compiten 6 listas, las que obtienen menos del 8.3% de los votos no tendrán representación. Esto podría dar la impresión de que, para tener alguna chance de representatividad, es más conveniente que compitan muchas listas. Pero visto de forma panorámica, como se ilustra en la Figura 1, los umbrales Ln,h se desplazan hacia la izquierda a medida que compiten más listas, alejándose de los umbrales Sh para h cercanos al total de sillas a repartir[10]. Por lo tanto, para las listas que tienen proporciones de votos “altas” (mayores, por ejemplo, al 50%), sobrepasar los umbrales de representación se hace “más fácil” a medida que compiten muchas listas, no así para las listas “pequeñas”.
Figura 1
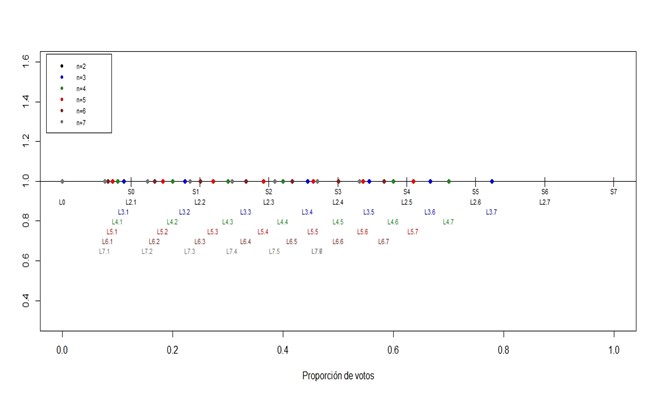
Los resultados expuestos permiten a cualquier movimiento o agrupación social, así como a cualquier partido político, analizar diversos escenarios basado en lo que creen que ocurrirá con las intenciones de votos de los electores. Para ilustrar este punto, usaremos como ejemplo el distrito 12 (que incluye las comunas de La Florida, La Pintana, Pirque, Puente Alto y San José de Maipo) y la elección de diputados de 2017, en la que compitieron 7 listas para elegir 7 diputados. Vamos a asumir que los electores de ese distrito se comportarán igual que entonces. Dicho comportamiento (incluyendo los votos nulos o blancos) está resumido en la siguiente tabla[11]:
Si la lista R fuese, para la realidad política del distrito 12, una lista independiente y obtiene esa cantidad de votos, entonces no superaría el umbral de representación L7,1 = 0,077, por lo que es seguro que no obtendrá escaño alguno. Por otro lado, si la lista G y la lista B fuesen unidas, asumiendo que los electores tendrán el mismo comportamiento el 11 de abril próximo, entonces esta nueva lista superaría el umbral S1 = 0,250, por lo que obtendría con seguridad al menos 1 escaño. Si la lista N fuese unida con la O (como algunos dirigentes de la antigua Concertación impulsan), la fuerza electoral correspondiente no alcanzaría para superar el umbral S1, aunque sí el umbral L7,1, por lo que es probable que se obtenga 1 escaño. La lista P se constituyó como la lista más fuerte de dicho distrito en el 2017. Si ella logra unirse a una agrupación que represente el 4% de los votos (siempre pensando que lo ocurrido el 2017 será semejante al 2021), entonces superarían el umbral S2 = 0,375, obteniendo con seguridad al menos 2 escaños. Todo esto, insistamos, suponiendo que compiten 7 listas. También se puede observar que, si estamos dispuestos a creer que los electores se comportarán en 2021 como lo hicieron en 2017, solo las listas fuertes (es decir, con una fuerza electoral al menos mayor al umbral S1) obtienen escaños: las más pequeñas, a pesar del esfuerzo político, no obtienen escaño alguno.
Los resultados generales, así como la ilustración, enfatizan cuán conveniente es conformar listas fuertes, es decir, listas que conciten el respaldo de muchos electores de manera que la fuerza electoral supere el umbral S1 y, más fuerte aún, S2 o S3. De acuerdo con la Ley 21.200, los distritos electorales eligen entre 3 y 8 representantes. En un distrito que elige 3 escaños, una lista obtendrá al menos 1 escaño si obtiene más del 25% de los votos; en un distrito de 4 escaños, debe obtener más del 20% de los votos para tener al menos 1 representante; en uno de 5 escaños, más del 16.7%; en uno de 6 escaños, más del 14.3%; en uno de 7 escaños, más del 12.5%; y en uno de 8 escaños, más del 11.11% de los votos.
Lo que sugiere el método de D’Hondt es que se requieren listas 'fuertes', es decir, listas que conciten una gran cantidad de votos, lo que a su vez significa asociarse en torno a ideales e intereses políticos lo más transversales posibles
La tarea se torna difícil tanto para listas de partidos políticos, como para las listas de independientes, es decir, de asociaciones de ciudadanos en torno a un interés común que no se percibe bien representado por los partidos. Ciertamente, puede parecer menos difícil para los partidos si se tiene en cuenta su maquinaria electoral, pero haciendo explícito un supuesto básico (repetido majaderamente en las simulaciones que hemos hecho): que los electores se comportarán como lo han hecho en elecciones pasadas. Para los independientes, pareciera que la esperanza se cifra en lo que ocurrió el 25 de octubre pasado, suponiendo que la opción por la CC se interprete como optar por una renovación radical de la política. Cualquiera sea el caso, hay un aspecto que es necesario enfatizar: la representación política en la CC es una representación de listas, es decir, de ciudadanos y ciudadanas que se agrupan en torno a intereses comunes que se pretende plasmar de una u otra manera en la redacción de la Nueva Constitución. Hoy parece posible una renovación de la política solo si prevalece, por un lado, la conciencia de lista y, por otro, la conciencia de que nuestro sistema electoral privilegia las “fuertes”.
Hace casi 170 años, el 26 de noviembre de 1842, Domingo Faustino Sarmiento, declarado ciudadano ilustre, fundador de las Escuelas Normales en Chile, contrastaba, en El Mercurio de la época, a propósito de las dificultades que veía para financiar las escuelas primarias en Valparaíso, “el espíritu de asociación”, esa fuerza de asociarse por intereses comunes para sacarlos adelante, con lo que parecía mover a los chilenos: “somos muy susceptibles de ser impulsados al bien y somos dóciles a la voz del gobierno o de un hombre de genio que propone, inculca y se empeña en la realización de una idea útil”. Aún hay tiempo de superar esta antigua conciencia de caudillo (que hoy por hoy bien podría estar representada por los esfuerzos, conscientes o no, de los partidos por atraer a los independientes). Pero, insistamos, se requieren asociaciones de grandes proporciones. Las herramientas para hacer algo de “ingeniería electoral” están disponibles: solo falta que dichas asociaciones y movimientos se manifiesten.
Arendt, H. (2016/1954). Verdad y Política. En: H. Arendt, Entre el pasado y el futuro. Ocho ejercicios sobre la reflexión política. Capítulo VII. Ariel, Buenos Aires. Titulo original: H. Arendt, Between Past and Future, Penguin Books.
Ballinski, M.L. & Young, H.P. (1975). The Quota Method of Apportionment. The American Mathematical Monthly 82, 701-730.
Birkhoff, G. (1976). House monotone apportionment schemes. Proceedings of the National Academy of Science 73, 684-686.
D’Hondt, V. (1882). Système pratique et raisonné de représentation proportionnalle. Librairie C. Muquardt, Bruxelles.
González, J. & San Martín, E. (2018). An alternative view on the NEAT design in test equating. In: Marie Wiberg, Steven Culpepper, Rianne Janssen, Jorge González, Dylan Molenaar (Eds.), Quantitative Psychology: The 82nd Annual Meeting of the Psychometric Society, Zurich, Switzerland, 2017. Springer Proceedings in Mathematics & Statistics, 233, 111-120.
Huntington, E. V. (1921). The Mathematical Theory of the Apportionment of Representatives. Proceedings of the National Academy of Sciences 7, 123-127.
Huntington, E. V. (1928). The Apportionment of Representatives in Congress. Transactions of the American Mathematical Society 30, 85-110.
Lijphart, A. & Gibberd, R.W. (1977). Thresholds and payoffs in list system of proportional representation. European Journal of Political Research 5,219-244.
Lynch, M. (2018). Éloge de la raison. Pourquoi la rationalité est importante pour la démocratie. Agone.
Manski, C. (2011). Policy Analysis with Incredible Certitude. The Economic Journal 121, F261-F289.
Maza, J. (1913). Sistemas de sufragio i cuestion electoral. Segunda edicion. Imprenta “La Ilustración”, Santiago.
Palomares, A. & Ramírez, V. (2003). Thresholds of the divisor methods. Numerical Algorithms 34, 405-415.
Pukelsheim, F. (2014). Proportional Representation. Apportionment Methods and Their Applications. Springer, New York.
San Martín, E. (2020a). El Sistema de D’Hondt ¿Cómo funciona y qué significa? (DP2020-05). Laboratorio Interdisciplinario de Estadística Social LIES, Pontificia Universidad Católica de Chile. (https://lies.mat.uc.cl/wp-content/uploads/2020/11/DP2020 05.pdf).
San Martín, E. (2020b). ¿Cómo presentar imparcialmente los resultados del plebiscito? El caso del distrito 11 (DP2020-04). Laboratorio Interdisciplinario de Estadística Social LIES, Pontificia Universidad Católica de Chile, Chile. (https://lies.mat.uc.cl/wpcontent/uploads/2020/11/DP2020 04.pdf).
San Martín, E. (2020c). Las posibilidades de elegir convencionales según el Sistema de D’Hondt (DP2020-06). Laboratorio Interdisciplinario de Estadística Social LIES, Pontificia Universidad Católica de Chile, Chile. (https://lies.mat.uc.cl/wpcontent/uploads/2020/11/DP2020 06.pdf).
San Martín, E. & González, J. (2020). How Fair is to be Fair? Revisiting Test Equating under the NEAT Design (DP2020|01). Laboratorio Interdisciplinario de Estadística Social LIES, Pontificia Universidad Católica de Chile. (https://lies.mat.uc.cl/wp-content/uploads/2020/11/DP2020 01.pdf).
[2] En este distrito, la lista P (esencialmente Chile Vamos) obtuvo 5 escaños, mientras que la lista G (esencialmente Partido Humanista y Revolución Democrática) obtuvo 1 escaño.
[3] Para detalles y ejemplos del método de D’Hondt, ver San Martín (2020a)
[4] Siguiendo a Hannah Arendt (2016/1954), una verdad de hecho se caracteriza por el hecho que su opuesto no es el error o la ilusión, sino la falsedad deliberada o la mentira. Así, por ejemplo, una mentira en relación a lo que ocurrió en el plebiscito del 25 octubre sería afirmar que, entre los que votaron, tanto la opción por CMC como CC estuvieron reñidas. Otro ejemplo es al que hace referencia Michael Lynch en el prefacio a la edición francesa de su libro In Praise of Reason: Why Rationality Matters for Democracy (Lynch, 2018): “a finales del mes de enero de 2017, el portavoz del nuevo presidente de los Estados Unidos declara que la multitud reunida para la investidura de Donald Trump era la más grande que se haya visto para una ocasión similar. Esta afirmación era falsa […] había innumerables pruebas fotográficas que probaban lo contrario […]” (p. VII). La verdad de hecho es que la multitud reunida no era la mayor de la historia de las investiduras. Como afirma Hannah Arentd, no se trata de juzgar estas falsedades o mentiras desde una perspectiva moral, sino entender el rol que juegan dichas afirmaciones en la acción política.
[5] Los porcentajes están calculados teniendo en cuenta los electores que votaron en blanco o nulo.
[6] Existe un sinnúmero de procedimientos estadísticos tendientes a imputar los datos faltantes o corregir sesgos de autoselección. Sin embargo, se trata de técnicas que, en el fondo, asumen que el problema no existe si se condiciona sobre variables relevantes. Para una crítica de esta postura en medición educacional, ver González & San Martín (2018) y San Martín & González (2020); para una crítica en políticas públicas en general, ver Manski (2011).
[7] Para una demostración de estas afirmaciones, ver Palomares & Ramírez (2003).
[8] El distrito 5 incluye todas las comunas de la Región de Coquimbo; el distrito 9 incluye las comunas de Cerro Navia, Conchalí, Huechuraba, Independencia, Lo Prado, Quinta Normal, Recoleta y Renca; el distrito 12 incluye las comunas de La Florida, La Pintana, Pirque, Puente Alto y San José de Maipo; el distrito 17 incluye las comunas de Constitución, Curepto, Curicó, Empedrado, Hualañé, Licantén, Maule, Molina, Pelarco, Pencahue, Rauco, Río Claro, Romeral, Sagrada Familia, San Clemente, San Rafael, Talca, Teno y Vichuquén; y el distrito 23 incluye las comunas de Carahue, Cholchol, Cunco, Curarrehue, Freire, Gorbea, Loncoche Nueva Imperial, Padre Las Casas, Pitrufquén, Pucón, Saavedra, Temuco, Teodoro Schmidt, Toltén, Villarrica.
[9] Tratamos indistintamente las proporciones como tales o como porcentajes.
[10] Para otros ejemplos y tablas correspondientes a H=3, 4, 5 y 6 sillas, ver San Martín (2020c).
[11] La lista B incluye Progresistas e Independientes Progresistas; la lista G esencialmente corresponde al Frente Amplio; la lista M corresponde a Unión Patriótica; la lista N esencialmente incluye el PC, PPD y PS; la lista O agrupa a laDC; la lista P esencialmente incluye Chile Vamos; y la lista R es una Candidatura Independiente.
Este artículo es parte del proyecto CIPER/Académico, una iniciativa de CIPER que busca ser un puente entre la academia y el debate público, cumpliendo con uno de los objetivos fundacionales que inspiran a nuestro medio.
CIPER/Académico es un espacio abierto a toda aquella investigación académica nacional e internacional que busca enriquecer la discusión sobre la realidad social y económica.
Hasta el momento, CIPER Académico recibe aportes de seis centros de estudios: el Centro de Estudios de Conflicto y Cohesión Social (COES), el Centro de Estudios Interculturales e Indígenas (CIIR), el Centro de Investigación en Comunicación, Literatura y Observación Social (CICLOS) de la Universidad Diego Portales, el Núcleo Milenio Autoridad y Asimetrías de Poder (NUMAAP), el Observatorio del Gasto Fiscal y el Instituto Milenio para la Investigación en Depresión y Personalidad (MIDAP). Estos aportes no condicionan la libertad editorial de CIPER.
CONTENIDO RELACIONADO
“Las mujeres pobres concentran la sintomatología depresiva en Chile”
Me sumo a lo comentado por Marco Antonio., agregándole que es tal el nivel de descomposición de de las instituciones estatales (gobierno, parlamento Poder judicial, contraloría y ahora el TC) que la ley, la razón y la verdad no tienen valor alguno, sólo importa satisfacer a una masa vociferante, que carece de la mas mínima capacidad de análisis, ideologizada a tal extremo que solo sigue consignas.
Marco Antonio | 21.03.2021
Han leído la actual constitución ? Ni la inflaron porque era mas facil quejarse y tirar piedras. En la actual se garantiza educación de calidad, lo que pasa es que el estado ya es tan grande que se fuma todos los recursos Y los alumnos son como la callampa, No le dan pelota al profesor cuando dicta clases. En todos los colegios pasan sumas, restas, álgebra, estadística, etc. Si los niñitos revolucionarios estudiaran en vez de salir a quemar locales comerciales, rendirían bien en los exámenes y se vería que de ellos depende la calidad educativa. Lo mismo para la salud, Los tipos no hacen ejercicios, comen como cerdos, ingieren azúcar todo el día y luego andan con cara de papi estado ayúdame a curar mi salud. Respecto a las AFP... ¿cuanto lograrían juntar cada uno si no fuera obligatorio imponer? R: CERO, se la gastarían toda en plasmas de 60 pulgadas.
Respecto a la delincuencia... Todos comprando en el comercio ambulante fomentando polos de asaltos, mugrerío, etc. Ahora respecto a las elecciones, ¿Quien ha confeccionado tablas de canditados, pactos, etc para poder votar informado ? R: NADIE. El Chileno se está acostumbrando a ganar lo mas posible con el mínimo esfuerzo. Si no le dan en el gusto, patalean, queman, roban, rayan, etc. AHORA todo lo descrito se fue mas al carajo con la inclusión de 1/4 de gente extra de otros paises que vienen con una mano adelante y la otra atrás,.
Cesar Hormazabal Fritz | 15.03.2021
el análisis técnico electoral sobre el método D'Hondt es impecable. Las conclusiones políticas sobre el mismo es una basura. En especial el ultimo párrafo a modo de conclusión:
"... se requieren asociaciones de grandes proporciones. Las herramientas para hacer algo de “ingeniería electoral†están disponibles: solo falta que dichas asociaciones y movimientos se manifiesten.".
Lo que dicho en buen chileno, es auto-censurar y disolver políticamente las expresiones de múltiples minorías dentro del consenso de algún estatus quo mayoritario fuertemente financiado
Maria Luisa Vasquez | 18.01.2021
Gracias por el artículo. Una vez más la voluntad mayoritaria está sujeta a tantos factores que al final, favorecen solo a los intereses dominantes.
Hemos visto un verdadero espectáculo por estos días, y en ese contexto las incoherencias de la oposicion no solo fragmentada en múltiples listas, sino también llevando como candidatos a CC a muchas figuras televisivas, farandula y otros, que no se caracterizan por una acción impugnatoria sostenida y fundamentada al sistema. Y sí, figuras así y de interés, las hay, pero no las consideraron. Han primado los egos, la competencia ideológica, el afán por la próxima carrera presidencial, las ambiviones personales; en síntesis , se aferran burdamente al poder.
La historia tal vez tenga que narrar cómo en Chile se despilfarró una oportunidad única.
Luz | 13.01.2021
Hecho a propósito para mantener el status quo.... La mayoría de la gente quiere una nueva Constitución, pero la escribirán quienes se oponen a ella...
Habría que aclarar en el último párrafo que Domingo Faustino Sarmiento era argentino.
Nicolas Negrete | 08.01.2021
Bien mala la nota no concluye nada, se enreda en la serie q escriben
Es mejor ir en una lista? Q pasa con las divisiones de la lista? Etc
Así, por ejemplo, si una lista obtiene menos del S0 = 1,25% de los votos[9], entonces es seguro que no obtendrá escaño alguno. Si obtiene, por ejemplo, una proporción de votos mayor que S2 = 37.5% de los votos, es seguro que obtendrá más de dos representantes. Los umbrales Sh expresan cuán difícil es obtener más de h sillas; es más, esta dificultad no depende del número de listas que compiten.
