El recientemente publicado informe de la comisión Bravo propuso, en síntesis, un conjunto de tres propuestas en lo esencial excluyentes entre sí, las que denominaron A, B y C. La propuesta A mantiene el sistema de capitalización individual; la C considera un sistema de reparto, y la B un sistema mixto entre reparto y capitalización individual.
Teniendo claro estas tres propuestas, a fines de julio los 24 comisionados realizaron una votación para determinar el apoyo con el que contaba cada una, apoyos que quedaron plasmados en el informe final. De los 24 miembros, 12 votaron a favor de la A, 11 por la B y 1 por la C.
Así, lo que se difundió por la prensa y lo que han manifestado algunos miembros adherentes de la propuesta A, es que esta fue la “ganadora” por obtener el mayor número de votos. Los miembros de las propuestas B y C, por su lado, argumentaron (por ejemplo aquí) que no hubo ganador, sino dos soluciones de mayoría, pues ninguna propuesta tuvo el 50% más 1 de las votaciones.
A continuación abordamos esta controversia analizando los métodos clásicos de votación. Esta reflexión entrega una propuesta sobre cómo tratar el informe final.
EL PROBLEMA DE UN CRITERIO ÓPTIMO DE ELECCIÓN
Determinar una regla de votación óptima, o técnicamente la agregación óptima de preferencias individuales, es un problema de larga data. Ya en el siglo XVIII en Francia se pueden encontrar trabajos de Jean-Charles Borda y su contemporáneo Nicolas de Condorcet. A continuación se ofrece un análisis de las tres reglas de votación más famosas y sus resultados para este caso particular.
Mayoría a dos vueltas: Empate
Para determinar la propuesta óptima entre A, B y C, una primera opción es lo que tradicionalmente se conoce como “segunda vuelta”. Este mecanismo se utiliza cuando se debe elegir una sola propuesta, como es el caso de las elecciones presidenciales en Chile. En una primera vuelta, las dos mayorías serían A y B. Determinar A como la alternativa ganadora sería lo que se conoce como regla de pluralidad, lo que no evoca muy buenos recuerdos respecto a la historia de elecciones presidenciales chilenas (Salvador Allende fue electo según esta regla). Así, si se hubiera pasado a “segunda vuelta”, lo más probable es que las propuestas A y B hubieran terminado ambas con 12 votos cada una. Este resultado se obtiene suponiendo que quien prefiere la alternativa C preferirá la alternativa B en la segunda vuelta (donde la alternativa C no está disponible). Y esto no es muy descabellado de asumir pues es B la única propuesta que incorpora un componente de reparto en el sistema de pensiones.
Es decir, una votación de este tipo no lograría generar una alternativa de consenso, sino un empate.
Condorcet: Vacío
La regla de Condorcet requiere la existencia de una alternativa que gane por mayoría en la comparación con cualquier otra alternativa. Desafortunadamente, los datos que tenemos de la votación no son suficientes debido a que no sabemos las preferencias de los miembros de la comisión por cada alternativa separada.
Sin embargo, supongamos que los 12 miembros que prefieren un sistema de capitalización individual (alternativa A) tendrán como segunda opción un sistema mixto (alternativa B) y como último alternativa un sistema de reparto (alternativa C). De la misma manera, no es descabellado pensar que quienes prefieren la alternativa B preferirán como segunda opción la alternativa C antes que la A y quien prefirió la alternativa C preferirá la B antes que la A. Con estos supuestos, podemos saber si existe una alternativa que gana por mayoría a cualquier otra en una “votación” simple con dos alternativas.
Si verificamos, A comparada con B en el agregado tiene 12 personas que la prefieren (los que votaron A) y otras 12 que no la prefieren (los que votaron B y C). Así, no podemos concluir que A sea una alternativa ganadora por esta regla. Continuemos con C: en comparación con A hay 12 personas que prefieren A a C (los que votaron por A) y otras 12 que prefieren C a A (los que votaron B y C). Con esto ya sabemos que C tampoco puede ser un «ganador de Condorcet». Para completar el análisis, la comparación entre C y B sí entrega una preferencia agregada: 23 personas (la mayoría) prefiere B a C, ya que solo 1 prefiere C a A. Sin embargo, B no es preferido por una mayoría frente a A, por lo que no puede ser la alternativa escogida por esta regla.
Por lo tanto, en este segundo método no existe una alternativa ganadora (vacío).
Borda: Ganador
El método de Borda asigna un puntaje a cada alternativa de acuerdo a la clasificación de alternativas dada por los electores. Así, en una votación entre 3 alternativas, si un elector clasifica una alternativa como la mejor entonces le otorga 3 puntos a la alternativa en cuestión. De la misma forma, un elector que clasifica una alternativa en segundo lugar le da 2 puntos, y así las alternativas clasificadas en último lugar tienen solo un punto.
Bajo el supuesto que utilizamos para tratar de calcular el ganador de Condorcet, podemos calcular los siguientes puntajes.
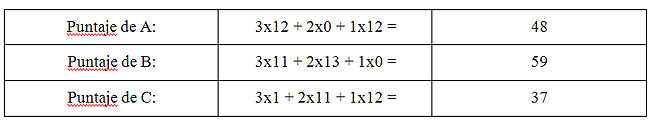
Hasta aquí lo único que supusimos fue un orden entre las alternativas. Aquí la alternativa B se beneficia del hecho de poseer componentes de ambas alternativas extremas. Cabe notar que incluso en el escenario más adverso para que gane B en este método, que sería el empate cuando los 11 que votaron B prefieran A antes que C, basta con que un solo miembro de esos 11 prefiera C antes que A para que gane B con el método de Borda. Desarrollos recientes en sistemas de votación por ranking más generales podrían también dar como ganador a B (ver Alejandro Corvalán, “How to Rank Rankings? Group Performance in Multiple-Prize Contests”, Mimeo).
Como conclusión, este método entrega como la alternativa óptima la propuesta B (ganador).
SOBRE REGLAS ÓPTIMAS DE VOTACIÓN
Dos siglos después de los desarrollos de Borda y Condorcet, el nobel en economía Kenneth Arrow concluirá en su tesis doctoral que no existe una regla de votación óptima si las alternativas a escoger son más de dos (ver Paradoja de Arrow). En efecto, la mayoría a dos vueltas, siendo el método más común para resolver este tipo de decisiones, no satisface dos de los criterios de optimalidad de una regla de votación según Arrow. Tampoco lo hacen los métodos de Condorcet y Borda.
El problema inicial, entonces, es someter un conjunto de más de dos alternativas a votación. En este caso, sabemos que la Paradoja de Arrow aplica, y no existirá una regla óptima. Aunque el mecanismo de votación por mayoría a dos vueltas convierta la elección en una decisión entre 2 alternativas (las dos ganadoras de primera vuelta) donde no aplica la paradoja, el número de miembros de la comisión no permite dirimir, al ser un número par (24 comisionados). Entonces, uno se pregunta, ¿por qué llevar a cabo una votación sin un mecanismo que lleve al consenso? Los resultados de la comisión, así como se han dado a conocer, dan para pensar que existe un grupo con poder de veto contra la alternativa B, o que habrá un miembro adicional (Presidenta) que zanjará el empate.
Otro punto importante, viene dado por las diferencias entre las preferencias al interior de la comisión de expertos y las de la ciudadanía. De hecho, en el Informe de Desarrollo Humano 2015 publicado por el PNUD, el 81% de la población cree que es mejor que el Estado se haga cargo del sistema de pensiones (propuesta C), el 15% opta por un sistema mixto (propuesta B), y solo un 3% prefiere un sistema de capitalización individual (propuesta A). En este sentido, más allá de la regla óptima de votación al interior de la comisión, un hecho importante es esta disociación entre la opinión técnica y la percepción ciudadana. Así, una condición necesaria para legitimar este tipo de reformas es hacer confluir estas dos visiones. Para esto, no sólo debemos hacer esfuerzos para que la información respecto de la toma de decisiones esté disponible, sino que dicha información sea accesible en términos pedagógicos a un público no técnico.
En conclusión, la votación hecha por la comisión no define una alternativa ganadora bajo ninguna otra regla distinta a la de Borda, siendo este el único método que produce un consenso: la propuesta B. Por otro lado, elegir la alternativa A es elegir una alternativa de no-consenso bajo cualquiera de las 3 reglas clásicas analizadas, lo que desestima el argumento sostenido por algunos de los miembros de la comisión en el sentido de dar por ganadora a la propuesta A. Dar por ganadora las 58 sugerencias de dicha propuesta implica seguir una regla de pluralidad según la cual gana quien saque más votos aunque no tenga mayoría. Por ejemplo, en la historia de nuestra democracia contemporánea, la enseñanza fue no repetir la regla de pluralidad, justamente por el peligro que el no-consenso genera para la convivencia social. Sin embargo, ex-post votación es difícil pensar que la comisión se pondrá de acuerdo en cambiar las reglas del juego sabiendo ya antes cuál será el resultado.
COMPARTIR
CONTENIDO DESTACADO
Andrés Chadwick aceptó que la fiscalía acceda a sus cuentas bancarias y al contenido de su teléfono
Lo correcto va por una administradora solidaria de pensiones, es decir una empresa social y no comercial como hasta ahora.
Una empresa social las utilidades que deja van a parar al fondo común de pensiones, en una empresa comercial como las de ahora van a parar directamente a los accionistas de este comercio, como son grandes utilidades estas empresa en pocos años recuperan y lo mas grave en estos de la especulación financiera les importa un rábano que los fondos acumulados den excelentes dividendo por una razón simple, no tienen responsabilidad alguna en el caso de pérdidas financieras.
Mucho se mal habla del pasado previsional sin considerar que en esos tiempo no existía personal o profesionales capacitados para dirigir esta famosas cajas, además en esos tiempo los políticos de la época hacían lo que querían con los ahorros provisionales acumulados por los trabajadores.
Hoy es distinto está la tecnología y profesionales capacitados para dirigir una empresa social solidaria y por supuesto con los controles adecuados para evitar desmadres..
Julio | 18.10.2015 | Socio/a 9 meses
La esencia del problema es el tipo de distribución del fondo al final del periodo; si su renta es superior esto no es garantía de que su pensión sea también superior en un sistema de reparto, no así en un sistema de capitalización individual, que por lo mismo tampoco es solidaria.
Una vez dirimido esto el problema será quien paga para cubrir la pensión mínima y una pensión medianamente decente
Carlos llanos | 18.10.2015
Los afiliados somos la razón de ser de las afp, nos sacan la plata a la fuerza y al amparo de la ley
O todos perdemos y todos ganamos según el ciclo económico o cambiamos el sistema
Mejoren primero la rentabilidad para el afiliado y después discutimos la edad y monto de la cotización
Carlos llanos | 18.10.2015
¿Quienos son estos expertos? Sabemos realmente si son o no independientes o accionistas de las afp. hay que investigar
Antes de gastar dinero en comisiones prohiban que los directores de las afp puedan ser también directores de las empresas en que las afp invierten
Sino es el gato en la carnicería
David Alvarez | 18.10.2015
Si el sistema es tan malo, entonces ¿como logré MM$ 60 a los 44 años, de los cuales yo puse sólo MM$ 16?
¿Tomarán mi esfuerzo y dedicación personal para repartirlo en una gran bolsa común?
Que cada uno asuma trabaje y construya su destino.
Ricardo Corona | 17.10.2015
Qué mejor solución que las personas escojamos qué sistema de pensiones queremos??? Esto se podría hacer, al menos, de dos formas: Coexistiendo los 3 sistemas (A, B y C), donde la posibilidad de elegir un sistema sería al menos periódica, pudiendo durante la vida laboral cambiar de un sistema a otro. Si prefieren que exista el mismo sistema para todos, entonces viene la segunda forma: Que se nos informe sobre las tres alternativas y NOSOTROS, como Pueblo, elijamos nuestra preferencia.
No creo que alguien argumente que sistemas de plebiscitos como los existentes en Suiza o los países nórdicos, o incluso en países más cercanos como Uruguay provoquen problemas sociales en vez de solucionarlos
Finalmente, me pregunto una vez más, ¿por qué no podremos escoger?? ¿Es legítimo que otros elijan por nosotros?? O será que tienen miedo... Mientras tanto, confió en algún momento ser dueño de mi destino.
José Perez | 15.10.2015
Esta claro que el actual sistema es un fracaso. Solo permite ganar a los accionistas de las AFPs. Cocentremos el interés en cambiar el sistema por uno qué solucione el problema de fondo las bajas pensiones.
luis avila barros | 15.10.2015
No más afp, sí a un sistema de reparto solidario y castigo a los ideologos del decreto 3500
Elías | 14.10.2015
Es lamentable que un pequeño grupo de personas, tengan la responsabilidad de elegir por sobre lo que desea la mayoría en este país.
También es atendible, el miedo que tienen las autoridades políticas de hacer cambios hacia un sistema de reparto, pues eso le quitaría de las manos a los señores que se han enriquecido con nuestros fondos y que lamentablemente nos amedrentan con sus discursos de siempre, es decir, campaña del terror, (aumento en la taza de desempleo, bajo crecimiento de la economía, etcétera).
Socio/a 9 meses
